[If the equations are not visible please try refreshing the page]
A linear transformation f is a transformation maintaining the following two properties:
Any linear transformation can be represented using a matrix multiplication with a vector.
Any linear transformation 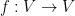 splits the n-dimensional space V into k f-invariant subspaces – direct sum of which returns the original space, V. These subspaces show eigenvector-like property i.e. when any vector
splits the n-dimensional space V into k f-invariant subspaces – direct sum of which returns the original space, V. These subspaces show eigenvector-like property i.e. when any vector  from such a subspace is transformed using
from such a subspace is transformed using  then
then
where 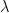 is a scaler value. Now, when all these f-invariant subspaces are one-dimensional, then the basis vector of each such one-dimensional vector is called an Eigenvector of the transformation
is a scaler value. Now, when all these f-invariant subspaces are one-dimensional, then the basis vector of each such one-dimensional vector is called an Eigenvector of the transformation  .
.
Notice that if the factors of m(f) are linear and distinct then kernel (or Nullspace) of each factor of m(f) is a one dimensional subspace (i.e. it has only one vector as basis). This vector is known as the eigenvector of the transformation f. If the transformation, f is expressed in terms of these eigenvectors (refer to change of basis theorem), it (the transformation f) will be turned into a diagonal matrix. That is why, matrices having distinct linear factors in its minimum polynomial is called a diagonalizable matrix.
If the factors are not distinct (i.e. like this, 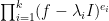 where
where 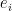 > 1) then
> 1) then  is the zero map on that ith invariant subspace. But for any power less than
is the zero map on that ith invariant subspace. But for any power less than 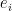 it will not be a zero map. From this phenomena, a new kind of transformation matrix is formulated – nilpotent matrix. It is defined as a matrix (or linear mapping/transformation) f, where
it will not be a zero map. From this phenomena, a new kind of transformation matrix is formulated – nilpotent matrix. It is defined as a matrix (or linear mapping/transformation) f, where 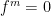 for a positive integer m.
for a positive integer m.
For any Nilpotent Matrix there exists an ordered basis with respect to which it (the Nilpotent Matrix) becomes a strictly upper triangular matrix.